１　１次関数の利用--- 図形ソフトを関数学習に利用して ---

（中学校 第２学年 数学）
東京都立田柄高等学校 坂本正彦

２．課題の設定

　関数についての学習は，中学校１年次に，ともなって変わる２変量として，比例，反比例の関係を学習し，中学校２年次で，一般的な１次関数を学習する。この後，３年次で頂点が原点にくる放物線を２次関数として学習した後，簡単にいろいろな関数について触れる。当然のことながら数学の教科書ではこの枠組みを逸脱することはあり得ないし，通常は授業もこの枠組みに沿って行われる。このような枠組みを設定することについては概ね賛成であるのだが，例えば１次関数の利用の単元において，扱われる例題や課題がすべて１次関数で表されるものしか取り扱っていないところに不満を持っていた。「２変量の関係が１次関数になっている例としてどのようなものがあるのか」という問題と，「ある２変量の関係をグラフ化した場合に，１次関数のグラフの性質を満たしていることからその２変量の関係は１次関数で表すことができると推定し，判定する」という問題は，１次関数を学習する上で重要な２本の柱であると考える。しかしこれまでは，学習者が獲得した知識を，順序よく積み上げていこうとすることを優先するがために，未学習の１次関数以外の関数について取り扱うことはためらわれてきたといえる。だが，テクノロジーの発達とその活用によって，身近な具体例の中に，データを収集することが可能となってきた。とくに本稿では，同じ中学校２年次に学習する平行四辺形をはじめとする図形の問題を，関数関係を理解するための場面として取り扱い，図形の中にひそむ２変量の関係を調べ，どのような場合に１次関数で表せる関係となっているかを考察する学習を試みた。

３．使用ソフトの概要

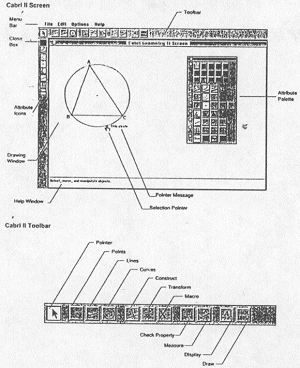
図１　Cabri�U　の初期画面

　Cabri Geometry�U 日本テキサスインストルメント株式会社

　もともと Cabri Geometre は，グルノープル大学のラボルデ教授が開発した幾何学習用のソフトでＭａｃ版とＤＯＳ版とがあり，日本語化はＤＯＳ版について筑波大学が行った｡この初代 Cabri の改訂に，テキサスインストルメント社が参加し，現在通称Cabri�Uとして，Ｍａｃ版とＤＯＳ／Ｖ版が発売されている（発売元は株式会社Ｎａｏｃｏ,tel:042 -521-1830）。現在はＷｉｎｄｏｗｓ版の開発が進められており，本稿で使用したのは，このＷｉｎｄｏｗｓ版のβ版である（図１）。Cabri�Uになって，特に面積の測定，計算が行えるようになった点を強調したい。尚デモバージョンは，ＴＩのＷＷＷページからダウンロードすることが可能である。（http://www.ti.com/calc/docs/cabri.htm）

４．授業の概要と経過

(1) 生徒の既習事項習と課題設定

　本学習に入る前に，生徒たちは既に以下のことを既習している。

1) ｙがｘの関数でｙ＝ａｘ＋ｂで表されるときに，ｙをｘの１次関数であるという。

2) １次関数では変化の割合が一定（＝ａ）である。

3) １次関数のグラフは直線となり，グラフが直線となる関数は１次関数である(除く　ｘ＝ｃのタイプ）。

4) １次関数の変化の割合は，グラフの中では直線の傾きとなっている。

5) 直線上の点が２点与えられれば，方程式が求められる。

6) ２直線の交点は，２直線の方程式を連立させたときの解となっている。

　即ち，関数関係として１次関数を学習し，また，その場合のグラフは直線になることを知っている。逆にグラフが直線となる関数は１次関数であることを知っている。そこで，ある事象から２変量の変化を測定し，そのデータをグラフに取ることで，２変量の関係が１次関数で表せるか否かを判定させ，図形の中ではどのような２変量が１次関数となっているのかを考察させる課題を設定した。

(2) 例題

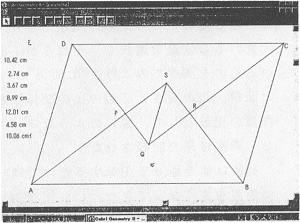
図２　平行四辺形の角の二等分線の問題

　図２のように，平行四辺形ＡＢＣＤの角の二等分線の交点Ｐ，Ｑ，Ｒ，Ｓを取る。このとき，□ＰＱＲＳは長方形となる。さてこの図において，点Ｄを動かすことによって，線分ＰＱと線分ＰＤの関係や，線分ＡＰと△ＰＡＤの関係，又は，線分ＡＤと□ＰＱＲＳの関係などを調べてみる。尚，点Ｄの動かし方も，辺ＡＢに平行に動かしたり，点Ａを中心とし，線分ＡＤを半径とした円周上を動かすなど，そのヴァリエーションもいろいろ考えられる。

図３　作図の手引き

　まずCabri�U上で，平行四辺形や角の二等分線といった条件を保ったまま，点Ｄが動かせる図を作図させた。生徒たちはまだCabri�Uに馴染んでいないため（これまでほんの数分触った程度であり，まともに自分で作図するのは今回が初めてであった。）図３のような手引きを配布した。丁度幾何分野の授業で，平行四辺形の定義や性質について学習したばかりであったため，手引きのように平行線の定義に則って作図せずに，例えば，「一組の対辺が平行で長さが等しい」というような性質に従って作図した者もいたが（予想以上に多かった），Cabriでは，独立に動かすことのできる辺や点といった基本図形と，それらから構成され，基本図形に従属して変化する図形とが明確に区別されている。よって，結果として静止状態では同じ図であっても，作図の手順や描き方の違いにより，全く異なった図形となることも少 なくない。例えばこの例では，平行四辺形を定義に従って作図すれば問題は起こらないがそうでない場合には，点Ｄを動かすことで，初めに問題で提示された条件が変わってしまう。本授業で学習させたい主題とは離れるが，平行四辺形の定義で用いられている条件と，そこから演繹される幾つかの性質とは，数学的には同値である。しかし Cabri の世界で様々な作図を経験してみると，図形本来の定義の重要性が再認識できる。たとえば平行四辺形の性質である「一組の向かい合う辺が平行で長さが等しい」でも，ノートに平行四辺形を作図することができるが，等長な辺の指定を注意しないと，点の移動によって平行四辺形が崩れてしまう。このことは，Cabri生んだユークリッド幾何の世界は，幾何学の体系が階層性を持って構成され構造化されてきたことを示唆しているとも考えられる。

(3) 計測と考察

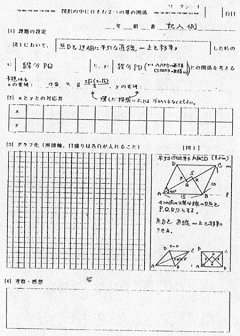
図４　ワークシート

　生徒の活動としては，まず例題について考察し，予め各自に出題しておいた「図形の問題を自分で選び，その中で伴って変わる２変量を選択し，それらが１次関数の関係になっているものを調べてみよう。」に従って，辺どうしの関係や辺と面積，辺の長さと２辺の比の関係などを調べさせた。また作業の記録として，図�Wのようなワークシートを複数枚配布し，測定結果を記録させた。

　初めは値を取って記録するだけで精一杯であったが，徐々に手際も良くなってきた。Cabri�Uでは，面積の測定も可能なため，三角比を知らない中学生であっても，線分ＰＤと□ＰＱＲＳの面積の関係を測定から考察することが可能となる。従来のCabri�Tでは，測定は線分の長さと角度しか行えなかったので，面積を測定するためには，その図形の面積の求める手順に従って補助線を沢山引かなくてはならなかったが，それが改善された。

　さて(2) の例題における２変量の関係は，例えば以下のようになる。

1) 線分ＰＱと線分ＰＤの関係は，１次関数ではない（三角関数を用いなくては表せない。）

2) 線分ＡＤと□ＰＱＲＳの面積の関係は，１次関数ではない（三角関数となったり２次関数となったりする。）

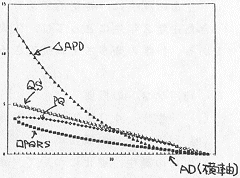
図５　辺ＡＤと線分ＱＳの関係

3) 線分ＡＤと線分ＱＳの関係は，１次関数で表せる（図５）。

測定した結果をもとにグラフを描くと，3)は直線のグラフとなる。つまり１次関数で表せそうだという予想が立つ。また，1)にあるように

隣り合う辺の関係は，１次関数にはならないということが予想される。およそ直線とは似ても似つかないグラフとなったからである。これは他の課題について取り組んだ生徒の考察とも一致する。また2)のように，辺と面積の関係も１次関数では表せないが，1)のような辺どうしの関係とも違うようである｡１次関数で表せられる関係としては，3)の他に，辺の比をとった場合などは，１次関数で表せる場合がある。

５．まとめ

　整関数の次元でいえば，１次関数は最も次数が低い関数である（２変量が隠れてしまうので，定値関数は除外しておく）。また，グラフの形状も直線となり，最も基本的で平易な図形として表される。それ故，直線にしても１次関数にしても軽視されがちであるが，日常生活の中でおこる様々な現象において，線形性はとても重要な性質である。この，線形性についての理解の基礎固めが，中学２年生で学習する１次関数ではないかと考える。そうだとすれば，初めに述べたように１次関数をとらえるということは，２つの量の対応関係という数の世界だけで学習させるのでは不十分ではないだろうか。筆者は，本稿で取り上げた課題のように，学習者自身が身近にとらえられる事象の中にひそむ２変量の関係に着目させる必要があると考える。これまでのチョークと黒板といったような静的なメディアしか無い時代ではやむを得なかっただろうが，例えば，Cabri Geometry�Uのようなテクノロジーを活用することで，学習者を取り巻く状況の中に問題事象を設定できるようになる。

　そもそも Cabri Geometry�Uなどの作図ソフトは，まず図形の学習に活用できるが，例えば作成した図形を基に課題を設定し，なにがしかの考察を加えるといった活用も可能である。寧ろ今後は，作図ソフトであるから図形の学習に，グラフ表示が可能なソフトであるから関数の学習に，といったステレオタイプな使い方ではないところに，テクノロジーの資産の活用のヒントがあるような気がする。

　最後に，本稿で扱った課題は，高等学校においても十分意味のある課題であると考える。高校１年生で２次関数を学習した時点でも可能であるし，２年次に三角関数を学習した時点でも，そのときに学習した知識を活用しながら，データ収集，分析，仮説設定，検証という科学の方法に沿った学習が行えるからである。