
聾学校におけるインターネットで活用できる動的教材の開発と実践
高等部・専攻科 数学
宮城県立ろう学校 中村好則
キーワード:聾学校,高等部・専攻科,数学,動的教材,DynamicHTML,VBScript
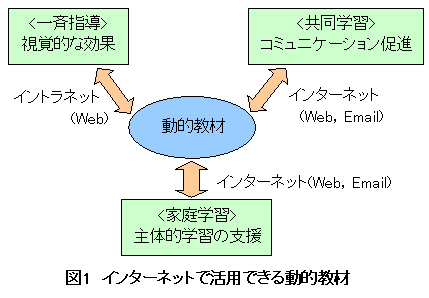 DynamicHTMLとVBScriptを使用し,動的教材をインタラクティブで動的なWebとして作成することとした。
DynamicHTMLとVBScriptを使用し,動的教材をインタラクティブで動的なWebとして作成することとした。
|
学習活動・内容 |
指導上の留意点 |
|
|
導入 5分 |
1) 「兄が家を出てから15分後に,弟が自転車で兄を追いかけた。兄の速さは毎分100mとし,弟の速さを毎分300mとすると,弟は何分後に兄に追いつくか」を提示する。 | 1) 中学部で学習した内容について復習をすることを告げ,提示されたような問題を覚えているかどうかを確認する。 |
|
展開 30分 |
2) 各自で解法を考える。 <予想される生徒の反応> ①1分毎の兄と弟の距離を考える。 ②方程式を利用し解法する。 100(15+x)=300x,x=7.5 ③図を書いて考える。 3) 考えた解法を発表する。 4) コンピュータを起動し,動的教材を見る 5) もう一度自分の解法について考え,修正が必要な場合は解答を修正し発表する。 |
2) 解法が分からない生徒は,問題場面を図に書いてみる。多くの生徒は②の解法を考えるのは難しいものと思われる。 3) 黒板に解答を記入し発表する。 4) 電子ボードを利用し全員で大きな画面で見る。その後,各自で操作してみる。 5) 黒板に書いた解法の修正個所は消さないで,別色のチョークで修正し説明する。 |
|
まとめ 15分 |
6) 動的教材の問題の条件を変え,問題を解く。 <変えられる条件> ①弟の出発する時間 ②弟の速さ ③兄の速さ 7) 分かったことをまとめ発表する。 |
6) 各自のコンピュータで操作しながら,自分で解いた問題はノートにまとめる。 7) 気づいたことをノートにまとめ発表する。 |
|
学習活動・内容 |
指導上の留意点 |
|
| 導入 10分 |
1) 「0から9までの数字が3つ並んでいるスロットマシンが2つある。どちらが当たりやすいか。(1)は7が3つでると1等,7が2つでると2等,7が1つでると3等。(2)同じ数字が3つでると1等,2つでると2等」を提示する。 2) どちらが当たりやすいかを予想し,理由とともに述べる。 |
1) 電子ボードに動的教材を起動し課題を提示する。 2) <予想される生徒の反応>
|
| 展開 40分 |
3) 実際に,動的教材をもとに多数回の試行をしてみる。 4) 実験結果と自分の予想を比較する。 5) 自分の実験結果を電子メールで共同学習の相手校に送る。 6) 共同学習相手校の実験結果の電子メールを受信し,自分の結果と比較し検討する。 7) 検討結果を電子メールで送る。 |
3) 1人1台のパソコンを利用して行う。 4) 実験結果について,理由についても考える。 5) 電子メールは共同学習のメーリングリスト宛に送り全員で共有できるようにする。 6) 共同学習相手校には,本時までに実験し結果を電子メール送信するように事前に依頼する。 |
| まとめ 10分 |
8) それぞれにスロットマシンについて確率を計算し,実験結果と比較する。 | |
| 8) 計算結果は,スロットマシン(1)は0.271,スロットマシン(2)は0.28となる。 |
3. 実践の様子と成果
(1)実践事例1(文章題の指導)・・・「視覚的な効果」
 |
 |
 |
 |
文章題の指導では,情景図や線分図などの静的な教材を手立てに指導する場合が多かったが,このような静的な教材は変化する諸事象の関係を捉えることが難しい。しかし,動的な教材は,事象の変化に対応して,変化するものを視覚的に捉えることができ,問題場面や数学的な意味の理解を支援できるものと思われる。
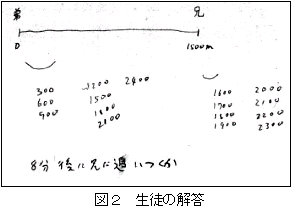
実践事例1では「兄が家を出てから15分後に,弟が自転車で兄を追いかけた。兄の速さは毎分100mとし,弟の速さを毎分300mとすると,弟は何分後に兄に追いつくか」という問題について考えた。対象生徒(高等部2年生)は中学部で方程式による解法をすでに学んでいるが,図2のように1分毎の弟と兄の移動距離を考え,解答を「8分後に,弟は2400m,兄は2300mだから8分後に追いついた」とした。実際には8分後には弟は兄を追い越しているが,そのことに気づいていない。
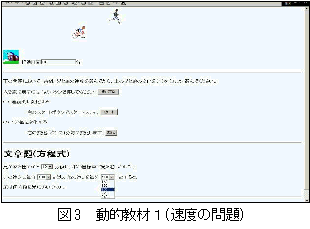
しかし,問題の条件と同じように動く動的教材(図3)を使うことで,8分後には弟はすでに兄を追い越していることや8分後より前に追いついていることに気づき,正しい解答を考え直す機会となった。また,この教材では弟の出発時間や弟や兄の移動する速度を変えることができるように作成されている。問題の条件を変えて問題を考えることで,問題の意味や構造の理解を促すことができたものと思われる。
(2)実践事例2(確率の指導)・・・「体験的な効果」
確率の指導では,「N回の試行で事象Aがr回起こったときの相対度数r/Nは,Nを増加するとある一定の値に近づく,その値を確率という」というように相対度数から考えた確率(経験的確率)を指導し,さらに確率について「同様に確からしいとき,P(A)=n(A)/n(S)(数学的確率)」と定義(ラプラスの定義)している。その意味を理解するためには,実際に問題の事象について多数回の試行を体験し経験的に理解することが重要である。しかし,聾学校では1クラスの在籍数が少なく多数回の試行が必要な実験や他の生徒の結果と比較するような授業を行うことが難しい。そこで,インターネット上においた動的教材を活用した共同学習を行うことで,共同で実験を行ったり実験結果を比較したりすることができる。
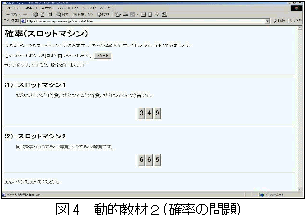
実践事例2では「0から9までの数字が3つ並んでいるスロットマシンが2つある。どちらが当たりやすいか。(1)は7が3つでると1等,7が2つでると2等,7が1つでると3等。(2)同じ数字が3つでると1等,2つでると2等」という問題について考えた。初めにどちらがあたりやすいかを予想してから,この問題と同じように当たりが出る動的教材(図4)を使って実際に実験を行った。その結果を「(1)を100回やったら25回も当たりました。(2)は(1)を上まわりし31回当たりました」というように電子メールでお互いに伝え合い意見交換を行った。他の生徒も(2)の方が(1)を上まわった。その後,試行の結果と計算結果((1)0.271(2)0.28)を比較し検討を行った。
4. まとめと課題
実践事例1からは,一斉指導において動的教材の活用は問題の意味の理解を視覚的に支援することができることが示唆された(視覚的な効果)。実践事例2からは,動的教材を共同学習で使うことで実験を共同で行うことができ,その結果について合同で検討を行うことができた。その結果,生徒同士のコミュニケーションが促進され体験的な理解を促すことができた(体験的な効果)。また,このような視覚的あるいは体験的な効果は,生徒の学習意欲を高め,主体的学習を促すことができたものと思われる。
動的教材は実践事例(1)(2)以外に,2次関数(平行移動,最大値と最小値,2次関数と方程式,2次関数の応用),個数の処理(自然数の列),微分積分(最大値・最小値の応用),平面幾何(軌跡)などを作成した。これらの教材を活用した指導においても,初めに問題について解答し,次に動的教材を用いてその解答を検討し意見交換を行うことで,視覚的にあるいは経験的に数学的な概念や意味の理解を支援できることが示唆された。
今後は,さらに多くのインターネットで活用できる動的教材を開発し実践を継続することと,表現内容や使用環境が限られているDynamicHTMLやVBScriptだけではなく,他の言語や方法なども活用し教材の開発を行うことが課題である。また,今回の実践研究では一斉指導や共同学習での実践を行ったが,インターネット上の動的教材を家庭学習で活用した実践については行っていないので実践し検討を行いたい。
|
ワンポイント・アドバイス 今回開発した動的教材はパソコンにインストール必要がなく,インターネット環境とWWWブラウザ(Internet Explorer)があれば動作する。パソコンやソフトウエアが授業の中心になるのではなく,授業の中で使いたい場面で簡単に操作でき,考えるための道具として使用することが可能である。 |