図形を等分する問題です。

   三角形ならば、一つの頂点と、対辺の中点を結べば２等分でき

   るから特に問題はありません。三角形の３等分も同じです。

     しかし、四角形になるとどうでしょう。三角形に等積変形し、

   三角形になおしてから、２等分、３等分するのなら、それでも可能です。 

   ここでの問題は、四角形のまま、２等分、３等分しようというのです。

   四角形が、正方形、長方形、菱形から、平行四辺形までなら簡単ですが、

　台形から先は工夫がいるようです。 

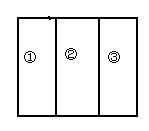
   台形ＡＢＣＤ(ＡＤ〃ＢＣ)ならば、平行な辺をそれぞれ、２等分、３等分し

  て結べば、面積の２等分、３等分ができます。(図１)

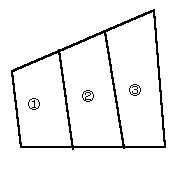
  これが一般の四角形ではどうなるのでしょう。

  ある人が、長方形と同じように、向かい合う辺を、それぞれ２等分、３等分し

  て結べばよい、と答えました。(図２、３)

  本当でしょうか。


     正しければ、正しい理由を、もし、間違っているのならば、

     反例(正しくない例)を示して下さい。



  また、四角形に条件があるのならば、どういう条件ならば、

  それが成り立つかを教えて下さい。 



  図１。　　　　　　　 　　　図２。　　　　　　　　　　 　　 図３。

  台形の場合 　　　　　　長方形の場合 　　　　　　　　一般の四角形