1.測定を取り入れた「チェバ及びメネラウスの定理」の指導

2.授業のねらい及び構成について

(1)授業の目的

　高等学校における数学Aの「平面幾何」では,学習の目的を「直観的な判断を基にし,論理的な思考や記述を通して理論を体系化していく能力を育成する」ことにおいている※1。ところで学習単元としての「平面幾何」は,昭和53年8月に出された学習指導要領から削除され,それ以降高等学校では扱われていない。解析的手法を用いて論理立てて演繹していくことを主にした高等学校の数学教育の中では,学習者の直感力に依存しがちな論証幾何は高等学校数学の学習体系に乗っておらず異端であるという見解や,論証幾何の指導では認知的な裏付けを持った指導が確立させておらず,解る者にのみ解る指導になりがちだという見解等幾つかの否定的な見解もあるが,論証幾何を学習する中で身に付く様々な習慣や,問題解決の方略の訓練に適しているという主張も同時に紹介されてきた※2※3。しかし,学習の意義がどのように高くとも,現実に学習しづらいという側面は無視できない※3。
　一方学校教育において,科学の方法や科学的思考の経験の重要性が強調されて久しい。科学は「諸現象について法則を立て,これを説明し,かつ将来を数量的に予測することを目標とする」学問である※4。本学習は,「メネラウスの定理」,「チェバの定理」が導かれた幾何学的現象をコンピュータ上に描き出して変化させ,元の三角形のそれぞれの辺の分点の比を数量的な変化として捉え,そこで生ずる3つの比の積が,計量的におよそ1となることを考察させ,次いでその考察が正しいことを数学的に論証する形で構成される。これは一般的に言われる「科学的な思考」を体験させるだけでなく,数学学習の目標である「事象を数学的に考察し処理する能力を高める」※5ことも目指している。

(2)授業の流れ

　元来,本単元での「メネラウスの定理・チェバの定理」の学習の目的は,中学校数学において学習した図形の基本性質をまとめ,それを総合して使いこなす点にあるが※1,本学習では,(1)で述べたように,両定理が示す幾何学的現象をまずコンピュータ上に実現し,そこから得られる計量的データを集約し,それらを基にこの数学的現象における法則性を計量的に推論する点に重点を置く。単に数学的事実である「メネラウスの定理・チェバの.定理」を既習事項から演繹するのではなく,学習者の操作的活動を通して「メネラウスの定理・チェバの定理」と呼ばれる現象を実体験させることで,学習者に問題事象に対する理解の深化を促すと同時に,操作活動を通して計測したデータによる経験的理解の曖昧さから生ずる数学的事実を認定しきれない不安を与えることで,これらの現象が数学的事実として認定できるための根拠として,次に幾何学的論証が不可欠であることを認識させる。

3.利用ソフト名

(1)利用ソフト

Cabri Geometre ver2.1(筑波出版会)及びLOTUS 1-2-3R4J(ロータス��)

(2)利用ソフトの概要

［図１］メネラウスの定理（２） ［図２］メネラウスの定理（２）

1) Cabri Geometre ver2.1(PC-9801周)

　CabriGeometreはフランス,グルノーブル大学(UniversityJosephFourierGrenoble)のJean-Marie.Labordeによって開発され,1993年に筑波大学の中山和彦,能田伸彦らによって日本語化された,トポロシカルな幾何学学習用アプリケーションソフトである。
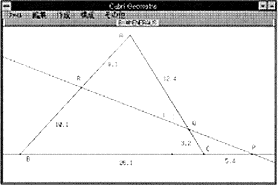
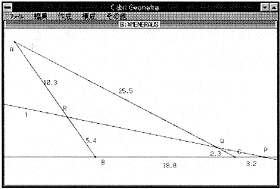
　右の図1,図2は,CabriGeometryにメネラウスの定理を表現する図を作図した状態である。作図の方法は,まず3点A,B,Cを取り,それを線分で結び,△ABCを作る[作成]。次に直線1を引き[作成],直線BC,CA,ABとの交点P,Q,Rを取る[構成]。最後に必要な線分の長さを表示するように設定する[その他一測定]。CabriGeometreの特徴は,ここで構成された△ABCと直線1の関係が,初めに作成した点の位置の如何に関わらず保存されると言う点である。即ちマウスにより点A,B,Cや直線1を規定する点であるP,Q,Rを画面上の何処に移動しても右の図が描かれ,また測定された線分の長さも逐一表示してくれる。このことにより,特別な状態から一般的な状態まで,様々な状態を観察することができる。但し,計算機能が無いので,得られたデータは手計算するか,別に計算用のアプリケーションを起動して計算する必要がある(ここではLOTUS1-2-3を使用する)。

2) LOTUS1-2-3R2.2J(MS-WindowsマシンではR4J)

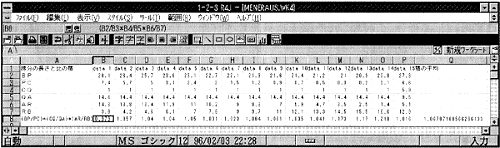
　本学習では,得られたデータの集計として,分点の比の値,その積の計算,それらの平均値の計算を行い(図3),更に視覚的に傾向を把握するためにグラフ化を行った。

［図�V］各線分の値と，内分・外分の比の積

4.コンピュータ利用の意図

(1)利用場面

1) 問題事象(ここでは「メネラウスの定理」)を,コンピュータ上で数学的現象として提示させる場面(CabriGeometre)
2) 提示された現象からデータを数量的に抽出する場面(CabriGeometre)
3) 抽出されたデータを数値計算し,計算結果を統計的に処理する場面(LOTUS1-2-3)

(2)利用環境

　模擬授業は,本校ではまだMS-DOSマシン(PC-9801/RX)しかないため,一人当たりCabriGeometre用に1台,LOTUS1-2-3用に1台の計2台を用いて行った。

5.授業実践

　本校では「平面幾何」はカリキュラムに組み込まれていないため,補習授業として対象となる生徒を,本校の理数コース1年生及び2年生の中から募って行った。

(1)学習指導案(学習指導案は「メネラウスの定理」用)

活動の目標	学習活動	注意事項
1) 問題事象の理解と作成	・CabriGeometre上にメネラウスの定理で用いる図形を作図させる。	作図の手順は提示しない。作図の順序は,学習者の問題の理解に依存する。但し,全体の進行を見て,提示するかどうか判断を下す。
2) データの抽出と整理	・予めLOTUS1-2-3を立ち上げておき,線分の長さを入力すると,それらの値から3辺の分点の比の積を計算させるシートが作成されているか確認させる。 ・マウスを操作しながら,考えられる様々な状態を作らせ,それぞれの場合の辺の長さを測定すしシートに入力する。	LOTUS1-2-3の使用方法は,本時の目標ではないのでこれについては予めワークシートを渡しておく。
3) メネラウスの定理の予想(法則化)	どのような三角形を作っても,どのような直線1を引いても,3分点の比はおおよそ1になることを確認させる。	誤差の大小はどのような場合かを確認させる
4) 数学的な証明	・幾何学習の既習事項を確認する。 ・時間を決めて,個別に証明させる。 ・証明ができた生徒に発表させ,質疑の後,どの証明がどの点で優れているのか考察させる。	学習者の様子を見て適時方略を示唆する。色々な解答についての評価を教師主導で行わない。
5) 定理のまとめと学習の考察	・定理の内容と変化させた図形の状態を確認する ・本時の自分の学習について評価させ,成功した要因,失敗した要因をまとめさせる。 ・授業についての感想を書かせる。	時間があれば,代表的な例,特異な例を紹介する。

(2)授業の経過

　コンピュータを用いた時間はおよそ25分であり,証明に10分,考察等に15分強と50分の枠を少々越えてしまった。当初の目標として,メネラウスの定理とチェバの定理の両方を取り上げたかったのであるが,操作活動を重視しようとすると,一斉授業の形式ではたとえ少人数であっても難しいといえる。生徒の学習状況から,学習目標を本授業ではメネラウスの定理一本に絞った。ただ,数人の生徒はチェバの定理をCabri Geometre上に作図し,図形を色々に変化させ考察まで行えていたことを付記する。

(3)補注

1) 本学習に参加した生徒は2学年にまたがり,また「平面幾何」の受講希望者を新規に募集して行ったため,学習に対する意欲は平均より高かったといえる。しかし参加した全ての生徒がCabriGeometre及びLOTUS1-2-3を初めて使用する者ばかりであったため,授業の前に予め30分ほどアプリケーションソフトの解説を行った。

2) 授業実践は1台だけであるが,MS-WlNDOWSマシンであるならば,１台でCabri Geometre(MS-DOS互換ボックス上で利用)とLOTUS 1-2-3が同時に利用でき,しかもその結果をクリップボードを介して一太郎などのワープロに張り込みレポートも作成可能である(尚,本稿はMS-WlNDOWS上で作成した)。

6.まとめ

　授業を受けた生徒の感想から,まずCabri Geometreの強力な機能に目を見張らされたということが伺えた。加えて,活動を通しながらメネラウスの定理が作る現象を目にすることで,定理が意味する概念の理解が促進され,ややもすると形式的に数式処理を行う学習では,見失いがちな「定理本来の意味」を常に意識しながら学習に取り組めたという感想は重要である。そしてこれまで学習してきた法則・定理についても,Cabri Geometreを用いて確認したいという希望が少なくなかった。ある状態を表現した幾何学図形の,関係を保存しながら変化させた様々な状態を,簡単な操作で実現できるCabri Geometreの機能について関心を持った者が多いということは,平面幾何の学習において定式化された論証を暗記し,その手法を身につけるといったいわば受動的な学習観から,「与えられた問題はただ解くだけではなく,一般化していくための重要な情報であり,また自分で作問するための基底である」とする能動的な学習観に変わるきっかけを与えたということが言えると考える。
　今後の課題として,集団学習としては学習しづらい論証幾何においてさえも,受動的な学習観から能動的な学習観へ変革させるような指導を体系化する必要があると考える。

(実践者　東京都立田柄高等学校　坂本　正彦)

参考文献

※1:文部省,高等学校学習指導要領解説数学編,1989.
※2:小平邦彦,幾何への誘い(書籍及びVTR).岩波書店,1989.
※3:坂本正彦,プログラミングを通した数学学習の指導についての実践的研究,1994.
※4:文部省,高等学校学習指導要領解説数学編,1979.
※5;文部省,高等学校学習指導要領,1989.