1.測定を取り入れた幾何学習の指導

2.授業のねらい及び構成について

(1)授業の目的

　別稿「測定を取り入れた『チェバ及ぴメネラウスの定理』の指導」でも述べたように,高等学校における数学Aの「平面幾何」では,学習の目的を「直観的な判断を基にし,論理的な思考や記述を通して理論を体系化していく能力を育成する」ことにおいている。しかし「平面幾何」は,学習者にとっては学習しづらい科目であり,また指導する教師にとっても幾何学的な事実とそれに伴う論証を伝達・解説するといった,通り一遍の授業に陥りやすく,本来「平面幾何」の学習が意図する「理論の体系化」を行い得る能力の育成にI寄与しているとは言い難いのが現状であった。「平面幾何」「論証幾何」の重要性が様々なところで語られてきたが,それ故現状を打破する手だてを講ずる必要性は急務である。
　一方本稿で述べるような測定を取り入れた平面幾何の学習では,得られた測定結果から法則性を予想し,予想された法則性を色々な条件の下でも成り立つことを検証する三とで科学的事実として認識し,認識した事実が正しいかどうかを数学的に論証するという道筋によって構成される。学習者には幾何学的事実を論証するまでに,測定を通して体験した数学的経験を,自分で証明したいという動機を引き起こさせた上で,論証指導を行う。こうすることで,数学的事実を単に数式等で「表書己された事実」としての理解ではなく,「経験的事実」として理解させることが可能になる。また,測定から打ち立てた法則は,あくまでも経験した事実について成り立っている法則であり,一般化するためには数学的に論証しなくてはならない。このことは数学学習の目的意識を学習者の中に根付かせることにもつながると考える。

(2)授業の流れ

　本稿では具体的な例として,「チェバの定理」を取り上げる。元来,本単元で扱う「チェバの定理」の学習の目的は,中学校数学において学習した図形の基本性質をまとめ,それを総合して使いこなす点にあるが,本学習では,

1) これらの定理が導かれた背景となる幾何学的現象をコンピュータ上に作る。
2) 図形を計量的に捉え,そこから得られる幾何学的事実を考察させる。
3) 計量的に集約されたデータから,数学的事実を推論させる。
4) 個別情報をいくら増やしても,数学的な真理としては認められないことを確認し,論証の必要性を認識させる。
5) 数学的な論証を行う。
6) 以上の活動をまとめる。

という経過をたどる。単に数学的事実である「チェバの定理」を既習事項から演緯するのではなく,学習者の操作的活動を通して「チェバの定理」と呼ばれる現象を実体験させることで,学習者に問題事象に対する理解の深化を促し,数学的論証の必要性を認識させると同時に,論証的な思考や記述を行わせる。この学習は,数学学習の目標である「事象を数学的に考察し処理する能力を高め」ることも目指している。

3.利用ソフト名

(1) 図形ランチBOXver2.2(創育)
(2) 利用ソフトの概要とCabriGe�petreとの比較

　図形ランチBOXは,CabriGe�petreと同様,指定した図形の関係付けを保存しながら角度や長さといった要素を変化させることが可能なアプリケーションソフトである。基本的な機能としては,[作図][移動][測定][条件][印刷]がある。
　[作図][測定][印刷]が行えることは,CabriGeometreと概ね同様である。図形ランチBOXの特徴は,[条件1と[移動1の機能である。

[図１］チェバの定理 △ABCの中の任意の位置に点Dを取る。 次にこの点と３頂点とを結んだ直線AD, BD,CDが元の△ABCの３辺との交点を E,F,Gとする。このとき 　AG　BE　CF 　─・─・─＝１が成り立つ。 　GB　EC　FA

　[条件]では,図形中で指定した線分,角度等を用いた条件式を設定することができ,更にその式の取る値を表示することができる。この機能はCabriGe�petreにはなく,別稿の「測定を取り入れた『チェバ及ぴメネラウスの定理』の指導」ではCabriGeometreの他にLotus1-2-3を必要とした。図形ランチBOXでは,概ね一つのソフトウエアの中で,図形の作成,辺の長さの測定,条件式の値の計算結果の表示を行ってくれる。更に[移動]では,作図した図形の一次変換が可能である。これらは活動を通した幾何学学習の幅を広げてくれる。　
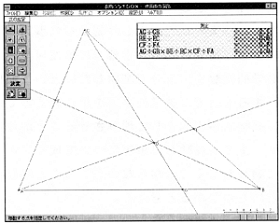
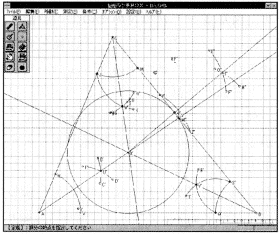
　右の[図1]は,図形ランチBOXにチェバの定理を作図した状態である。作図の方法は,まず線分AB,BC,CAを引いて∠ABCを作る[作図]次に点Dを取り(図形ランチBOXでは,作図の順にA,B,C,D,E,Fと割り振られるようである。この点は作図の順を予め考慮しなければならず,不便である。),各色頂A,B,Cから半直線AD,BC,CDを引く。半直線ADと線分BCの交点を点E,線分CAとの交点を点F,線分ABとの交点を点Gと指定する(図形ランチB()Xでは,図形の構成,関係付け,関係の取り消しができないため,この図で線分AE,BF,CGは作れない)。
　次に,[測定]若しくは[条件]で,AG:GB,BE:EC,CF:FAや,これらの積　AG÷GB×BE÷EC×CF÷FA………�@　を指定しすると,それらの値を[測定]若しくは[条件]([図1]では右上のウインドウの中)の中に計算してくれる。この測定値及び計算結果は,初めに指定した点A,B,C,Dのどれを移動しても再計算して表示してくれる。この機能はCabriGeometreには無い機能であり,測定を取り入れた平面幾何の指導では不可欠の機能である。ただ少数第一位までしか求めてくれないので(精度を上げることはできない),�@式は点Dの位置に関わらず常に!.0を示してしまい(まだ例外を発見していない),チェバの定理は明示されてしまい,学習者にとって推論の余地はない。一方,CabriGe�petreも測定値は少数第一位までの表示しないが,計算ができないためにLotus 1-2-3に取り込んで計算すると,少数第二位の値も表示でき(それ以下の値も表示されるが,有効桁数から外れるので意味がない),�@式が1.Oに近い数値になるため,法則が正しいかどうかを推論する余地が残される。筆者は測定を取り入れた平面幾何の指導としては,誤差を自動的に丸めずにそのまま表示させた方が良いと考えるが,どちらが良いかは指導目標の設定次第だと考える。ただ本課題のような場合はともかく,ソフトウェアが自動的に計算結果を丸めて表示する点が,本来正しくない結果を明示してしまう危険性を伴う点には注意しなくてはならないだろう。筆者はコンピュータの誤差を考慮しなかったが為に,誤った推論を行って袋小路に入り込んだ経験を持っている。勿論,図形ランチBOXとLotus1-2-3を併用すれば,同じ結果を得ることができる。　本稿で述べる具体的な学習指導計画については,別稿「測定を取り入れた「チェバ及びメネラウスの定理」の指導」に準ずるので,割愛する。

4.図形ランチBOXのその他の機能

［図２］２円に引かれる接線の様子

図形ランチBOXには,平面幾何の作図だけでなく,予め幾つかのシミュレーションプログラムが登録されている。
例えばメニューから平面幾何を選ぶと,転がる正多角形の各頂点の軌跡であるとか,三平方の定理の確認のためのシミュレーション,そして2円に引かれる接線の様子を表したシミュレーションなどが実行できる([図2])。
　その他,空間1図形の切断などを示すシミュレーションなどもある([図3])。このように図形ランチBOXは幾何学習において,非常に広範に利用することができるソフトウエアであるということができる。

5.作図機能についての私見及びまとめ

［図３］回転面の切断 ［図４］内心（CabriGeometre） ［図５］内心（図形ランチBOＸ）

　本稿ではチェバの定理の操作活動を通した証明の指導を扱ったが,これはその他の定理・法則でも同様の指導が行えると考える。
　さて作図に関することで些か指摘したい点がある。図形ランチBOXでは,作図の方法として円や多角形など予め部品として与えられた図形を組み合わせて作図する機能と,定規・コンパスという機能を組み合わせて作図する機能の2系統が用意されている。
そもそもユークリッド幾何では,定規とコンパスのみが道具として認められていることは今更指摘するまでもない。しかし初等幾何学も学習が進むに連れ,図形も複雑になってくる。このようなごく基本的な道具のみに依存するソフトウエアでは,学習活動を行う準備の段階で,作図の効率化が図れる様な配慮は重要な点である。例えば,線分の垂直二等分線,角の二等分線,垂線など基本的な作図ツールは備わっていても良いのではないか。学習の準備段階の時間的ロスを軽減することができる。
　実際に三角形の内心の作図を行ってみたところ,Cabri Geometreでは5分もかからなからたにも関わらず([図4]),図形ランチBOXでは20分以上かかって,しかも完成することができなかった([図5]では,円がきちんと内接していない)。定規・コンパスによる作図は,実際に紙の上で体験する方が重要ではないかと考える。
　以上の様な若干の問題もあるが,図形ランチBOXは中学校向けに開発されたにもかかわらず,高等学校の数学でも十分に活用できるソフトウエアであり,測定を中心にした幾何学習など,学習目的をはっきりさせて利用すれば,効果的に活用できると考える。