１ オリガミクスによる仮説−検証学習

２ 学習のねらい

　オリガミクスとは，紙を折ることによって生じる数理現象を研究する分野を意味し，同時にそのような数理現象そのものを指す言葉として，1994年11月に大津で行われた第２回折り紙の科学国際会議において提唱された※１。当初正方形の折り紙を素材に探求が進められたが，現在は三角形や1:√2など様々な多角形に拡張されて研究されている※１，※４。本稿では，紙を折ったり Cabri Geometre を活用しながら，そこに潜む数理を考察させ，「仮説の提案−演繹と予測−観察と実験」という科学の方法※５に従った活動を行わせる学習について述べる。これは学習指導要領でいう｢事象を探求する過程を通して，科学的，数学的に考察し，処理する活動｣※２に当たる。

　実際の学習では，まず規則性を探りながら折り紙を折り，何らかの法則性の発見に努める。必要に応じてコンピュータを活用し，打ち立てられた法則性の確からしさを検証し，最後に数学的に証明するという流れをたどる。

３ 利用ソフト名

４ オリガミクスの課題の分類と４頂点集中折りの解析について

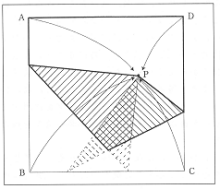
図１ ４頂点集中折り 図２ ４頂点集中折りの分布図

　オリガミクスで扱われる題材は，大きく２種類に分類できる※３。一つは予め設定した目標に向かって活動する「折り紙作図課題」であり，初等幾何学的に検証することが可能なもので，これまでに「仮説−検証−証明」型の学習が幾つも実践例として報告されている※４，※６。もう一つは「折る」回数を予め規定し，規定に従って折った結果を数理的に考察する「状態分析課題」であり，初等幾何で比較的簡単に説明できるものから，単純には証明できないものや，数列の収束・発散の知識を必要とするものなどが含まれ，高校数学やそれ以上の数学的知識及び問題解決方略が必要とされるもの※７も含まれている。また「状態分析課題」は，折り方が有限回か無限回かにより「有限試行課題」と「無限試行課題」とに分類される。このように分類されたオリガミクスの課題は既に60種類以上提案されているが，本稿では状態分析課題で有限試行課題である「４頂点集中折り」を取りあげる※１。　
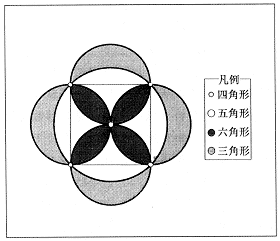
　「４頂点集中折り」とは，折り紙の中に任意の一点Ｐを取り，各頂点Ａ，Ｂ，Ｃ，Ｄを点Ｐに重なるように折った場合，折り紙の外形は，四角形以上の多角形になる。初めに取った点Ｐの位置によって折紙の外形が作る多角形の分類を考える（図１）。
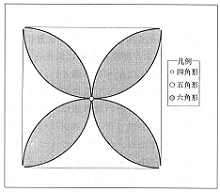
　４頂点集中折りの結果生じる多角形は，四角形，五角形，六角形（図２）である。実際に点Ｐを色々な場所に取りながら，何処に取ると五角形ができ，何処に取ると六角形ができるかという予想も，折り紙が正方形であることに着目すれば，正方形の対称性から各辺の垂直二等分線によって区切られる四分の一の正方形について調べればよく，更に正方形が対角線について対称であることを利用すれば，基の正方形の八分の一の直角二等辺三角形についてのみ調べれば良いことが解る。しかしこの学習では，これらのことも学習者による発見を待つことが必要である。正方形の対称性に気付いた生徒にとって，価値ある発見は活動の積極性を促進する。実際の学習では幾つかの段階に分けて行うのがよい。

(1) 予想の段階

　まず，折り紙を手に取り，適当に点Ｐを定めて折ってみる。何種類かの多角形ができあがったところで，法則性が見つけられるかどうかまとめさせる。このとき，点Ｐが対角線の交点に来ている場合であるとか，どこかの頂点にきている場合など，特別な場合についても確認ができると仮説をまとめやすい。

(2) 仮説検証の段階

図３ Cabri Geometre 上での分布

　この段階ではコンピュータでの検証が主になるが，新たな事実が発見された場合には再度折り紙での活動に戻ることが望ましい。
　まず点Ｐを折り紙の中を任意に移動させながら，できあがる折り紙の外形がどのように変化するのかを調査する。また点Ｐの分布図を予想することが個々の活動の目的となるが，結果を得るためには，コンピュータ上でアプリケーションソフトの活用のスキルに依存しがちである。ここでは CabriGeometre を利用するが，学習者が慣れていない場合には，習熟の段階に応じて活用できるプログラムを用意しておくことが重要である。そうでないならば，活動の意図が「４頂点集中折り」からCabri Geometrの利用に移ってしまい，学習の目的が曖昧になってしまう。 　
　具体的な操作としては，Cabri Geometreの中に軌跡という機能があるので，それを利用する（図３）。以上から図２を得た。

(4) 発展

図４ ３角形，５角形の分布

　さて，４頂点集中折りでは，まず正方形の内部に任意の点Ｐに４頂点を重ねるように折り，元の折り紙が何角形になるかを調べた。では点Ｐを正方形の外部に取ると，図形の分布はどのようになるであろうか。
　実際に折ってみると，点Ｐの位置により五角形や三角形ができあがる。次に CabriGeometre 点Ｐの位置を色々 に変化させてみると次のようになった（図４）。
　正方形は中心に対して点対称であるから結局三角形と五角形の境界線は，図５の様になることが予想できる。理由は(3)で示したとおりである。なお外側の４つの円の外には点Ｐは決して移動しない。なぜならば，移動する点Ｐと，最も近い頂点との垂直二等分線は，元の折り紙の外に引かれ，折り紙の上に折り線を４本引くことはできなくなるからである。これらの活動の結果，図５を得た。

５ まとめと展望

図５ 拡張４頂点集中折り

　こ れまで述べてきたように，オリガミクスによる科学的活動を取り入れた探求学習で一連の科学的思考過程を実際に体験し，自らが小さな科学者として活動する中で科学的考力を育成し伸長する場を提供する。そして操作的活動の結果得られたデータをコンピータ上にのせ，コンピュータがシミュレートする過程を観察することで，学習者は事象に対してより抽象的に思考することが可能となる。その中で実際の実験結果との矛盾が発生したならば，また具体的な操作活動に戻って法則性の確認を行う。このような態度や，実験による仮説−検証が行き詰まった時には数式で証明するという姿勢は，どちらも科学的活動※８，※９にはなくてはならず，それ故，科学的思考力の育成には不可欠の経験であると考える。　実験を通して精緻化された仮説や法則は，数式により証明することで正当性が立証できる。このような，数学の意義を経験する場面が数学以外の学習の中で強調されることは，数学教育の視点から見て極めて重要である※１０。
　実際に指導した生徒から，「理科で扱うような実験を行い，その結果を証明するのに数学が利用できたということは初めての体験であり，貴重な経験であった。」という感想が寄せられた。本来，理科であるとか数学であるといった分野の区別は，科学の歴史からみれは便宜的であったはずである。それ故，教科の立場にとらわれることなく，オリガミクスのような科学的探求活動の中で，最終的に数学の力によって正しさを立証するという学習は，もっと学校教育に取り入れられていくべきである。　これまで述べてきたことから，折り紙とコンピュータと数学とを連携させた学習が成立する「４頂点集中折り」や「直角螺旋折り」※１１のようなオリガミクスによる学習は，科学的探求活動を行うためばかりでなく，高等学校の数学で学習する数列の極限や三角関数の有用性を理解する上でも非常に有効な学習であると結論できる。今後は，オリガミックスの中の幾つかのトピックスを教材化するだけでなく，オリガミクスが一つの学習単元となるような体系化をはかることが必要であろう。

※1：芳賀和夫,オリガミクスによる科学教育の試み--「４頂点集中折りによる集中点の分布」題材の学習, 筑波大学学校教育論集第18巻,1995.

※2：文部省,高等学校学習指導要領解説,「数学科の目標」および「理科の目標」,1989．

※3：坂本正彦,芳賀和夫,オリガミクスによる科学教育の試み※２--コンピュータ，そして数学との関連についての一考察，筑波大学学校教育論集第19巻，1996.

※4：芳賀和夫,オリガミクスによる数学授業,明治図書,1996.

※5：竹内均,科学的思考とは何か，日本リクルートセンター,1983.

※6：芳賀和夫,筑波大学附属中学校における「課題学習」の実践,1993.10〜1994.3.（筆者はこのときアシスタントとして指導に参加した）

※7：芳賀和夫,田村良彦,任意三角形による７角不思議,オリガミクス研究会,1996.3.23.

※8：八杉龍一,科学とは何か,東京教学社,1991.

※9：板倉聖宣,科学と仮説,季節社,1971.

※10：坂本正彦,「科学の方法」をもとにした数学学習について,日本数学教育学会誌第77回大会総会誌, 1995.

※11：坂本正彦,オリガミクスによる科学教育の試み４--「直角螺旋折りに関する探求活動」,日本数学教育学会29回教育論文発表会論文集,1996.

［補足］図２は参考文献4より転載