１ 定義に基づいた導関数の学習

（高等学校 ２・３年 数学Ⅱ,数学Ⅲ）

２ 学習の意図

　高等学校における導関数の学習では，関数の値の変化を捉える一つの有効な方法を学ぶことを目的としている１。さて，導関数を求めるということは，予め定義された関数のそれぞれのxの値(x=a)に対して微分係数(f'(a))を対応させる関数を求めるということである。よって定義に従って計算されることが重要になるが，整関数や一部の特殊な場合を除いて，技巧的な計算を必要としたり筆算では困難であることも多く，高等学校の数学の中では指導の難しい単元の一つであるといえる。
　一方高等学校では，平成６年度末の時点で生徒の学習活用を目的としたコンピュータの導入率が８割を超えた２。同時にコンピュータの技術革新も進み，学習用に導入されたパソコンもMS-DOSマシンからWindowsマシン，マルチメディア・パソコンと進化し，同時にソフトウエアも高機能のものになってきている。そして実際にそれらが数学教育に活用され，報告されてきた３。これからもますますハードウエア，ソフトウエアとも高機能化したものが高等学校に導入され，それらが数学教育に活用されていくと考えられるし，筆者もそのことは重要であると考えている。
　ところでその高機能なソフトウエアの多くは，Mathematica に代表されるように簡単な記述で様々な計算をし，そのグラフを描画してくれる。導関数を求める場合にも，至って簡単な記述で実現できる。しかし高校生が初めて導関数の概念を学習する場合，これらの便利なソフトウエアにより計算した結果を明示しただけでは，学習として不十分となることは明らかであり，冒頭で述べたように，導関数とは微分係数の変化を表す関数である，という点を強調するような活用を考える必要が生じる。本稿では，この点に重点を置いた指導について報告するが，特に強調したいことは，このような学習は何も最新の高機能なハードウエアやソフトウエアが無くとも構成可能であるという点である。

３ 利用するソフトウエアと利用環境

(1) 利用ソフト名

1) Turbo Pascal ver.5.5 （ Boland Japan, MS-DOS版, PC-9801用）
2) Turtle Graphics Library４（ LOGOのライブラリィ ）

(2) 環境

　学習者は，NEC:PC-9801/RS (i80386sx 1.6MHz)をスタンドアロンで一人一台使用する。

４ 実践事例「導関数の学習について」

(1) 指導事例Ⅰ［導関数を描画するプログラムとその作符について］

関数の学習に汎用的に活用できるように，プログラムの構成を以下のようにした。
1) ［手続き］初期値の設定
2) ［手続き］xy-座標系の作成
3) ［関 数］関数の定義
4) ［関 数］与えられたx=aについての微分係数の計算
5) ［手続き］定義域内における点(x,f(x))の描画［y=f(x)のグラフの描画］
7) メインプログラム
1) ある正の定数hとdを定めて平均変化率を計算する。
2) |h|<dなるまでhの値を減じながらその都度平均変化率を計算する。
3) この操作を繰り返しながら，最終的な値を微分係数として採択する。
4) こうして計算した微分係数の値をy座標とする点 (a,f'(a))を描画する。
5) aの値を予め規定した値だけ増やす。
［関数の定義］ ［微分係数の計算］ 
function fx(x:real):real;
  begin
  if x<>0 then fx:=sin(x)/x;
  end;
 
function Dfx(x:real):real;
  var i, d, e, h, y: real;
  begin
    d := 0.01; e := 1/102
    4;
    h := 3; y := 0;
    while abs(h)< e do
      begin
        y:=(fx(x+h)-fx))/h;
        if abs(y) <=y_range
          then Ten(x,y);
        h:=h-d;
      end;
    Dfx:=y;
  end;
図１ 導関数のプログラムの抜粋，「関数の定義」及び「微分係数の計算」

(2) 指導事例Ⅱ［極値を与えるxの値と，導関数とx軸との交点との関係について］

1) 問題提起
図２ 極値と導関数の関係
y=k(x-a)(x-b)(x-c)のグラフ（a<b<c）のグラフを描画したとき，極値を与えるxは，グラフの中ではどのような値であろうか。
2) 仮説の設定と検証
実際に授業で発せられた順に仮説を紹介する。
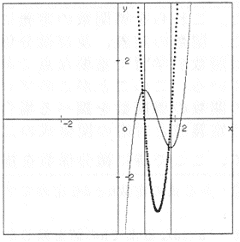
ht-1．x軸との交点の中点である。

この仮説が正しいと思っていた生徒たちも間違っていると考えていた生徒たちも，まずグラフを精密に観察し始めた。そして次にグラフの解像度を上げて実行したり，x軸との交点の中点を通り，y軸に平行な直線を同時に描画して，この仮説が間違っていることを実証した。どの生徒のコンピュータでも，x軸との交点の中点からは微妙にずれていることが観察された。

さて，次の手だてがなかなか見いだせないようなので，微分係数を基にグラフを描画するよう指示した。当初は，このグラフ（３次関数）と導関数のグラフ（２次関数）との関係に気付かないようであったが，解像度を変えながら色々試していくうちに，次の仮説をつぶやき始める者が増えてきた。
ht-2．導関数がx軸と交わる点のx座標の値が極値を与えるxである。

　筆者の方でまとめをするまでもなく，全員がそれぞれのコンピュータ上で，この仮説の正当性を実証する様子を確認した。では，何故そうなるのか。

3) 証明
　教科書にあるように証明を行ったが，生徒からは「コンピュータに映し出された時には不思議だったが，数学で証明すると納得できる」という旨の感想が寄せられた。結果として，ほとんどの生徒が証明について理解したようである。これは，自分でプログラムしコンピュータ上で視覚的に確認したということで，数式での演繹を行う最中でも，今何を計算しているのかを見失わないで済んだからのように思える。従来の教科書に沿った指導した時と比較して，この生徒たちの学習の定着の度合いは大変良かった。

(3) 指導事例Ⅲ［色々な関数の導関数について］

図３ y = sin x の導関数
　(1)で述べたプログラムに調べたい関数を定義すると，コンピュータは定義に従って計算し導関数のグラフを描画してくれる。コンピュータが描画したグラフの形状を基に，導関数の方程式を考察する。既知のグラフであれば，次にそのことを証明する。更に，パラメータの変化に応じて基の関数と導関数の変化を視覚的に確認しながら理解できるので，基の方程式の形と導関数のグラフの特徴についても考察することができる。以下 y = sin x を例にして述べる。
1) 仮説設定
プログラムの中で'y:=sin(x)'と記述すると，コンピュータは y=cos x らしきグラフを描く（図３）。これを仮説とする。
2) 証明
　和積公式を用いて導関数の定義の式から y'=cos x を導く指導を行った。ところで高等学校の学習単元のうち，公式の利用頻度が少ないことに加え，類似した式が幾つもあり，学習者に混乱をきたしがちな和積公式の定着は芳しくない。しかし，別の目的を達成する手段として扱う場合，利用目的がはっきりしているせいなのか，生徒たちはよく理解したように感ずる。この三角関数の和積公式・積和公式など，これまであまり活用の機会がなかった公式の利用は，学習者に技巧的であるとの印象を持たれやすい。しかしこのように探求したい事象を視覚化することは，学習しにくさを緩和することができ，何のためにこの計算を行っているのか，学習の意味を把握しやすくなると考えられる。それは従来の式変形による演繹では高度な抽象性が要求され，仮に式変形から演繹できた導関数も，多くはその形状が不明であることが多く，学習者にとって実在感が薄くなりがちだからである。
　実際に授業では，このプログラムの活用により，およそ60種類の関数とその導関数を調べることができた。

５．まとめ


※1：文部省,高等学校学習指導要領解説,1989.
※2：文部省,学校における情報教育の実態等に関する調査結果,'96教育用ニューメディア総覧,日本教育工学振興会,1996.
※3：礒田正美，佐伯昭彦，他,テクノロジーを用いた実験・観察アプローチ 1～14,数学教 育誌,1996.1～1997.2.,明治図書.
※4：坂本正彦,プログラミングを通した数学学習についての実践的研究,平成５年度東京都教育研究生報告書,1993.
CEC HomePage平成８年度市販ソフト実践事例集II