|
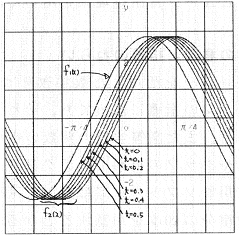
- f1(x)= m・sin x + n・cos x
- f2(x)= k・sin(x+t)
|
| y = m・sin x + n・cos x = k・sin( x + t ) ……… 1)
において,m, n, k, t の関係を調べる。 |

|
表1 実験記録シート
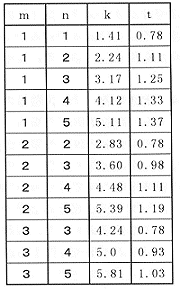 |
| ht-1: m = n のとき t の値が等しい
ht-2: m = n のとき m と kは正比例する |
| ht-3: m2+ n2= k2となる |

| ht-4: mとnの比 m/n が等しければ,tの値は変わらない |
(2) の仮説ht-3をもとに1) 式を考察してみる。
1) の右辺 = k・sin(x+t)
= √(m2+n2)・sin(x+t)
= √(m2+n2)・sin x ・cos t + √(m2+n2)・cos x ・sin t
= √(m2+n2)・cos t ・sin x + √(m2+n2)・sin t ・cos x ……… 2)
∴ m = √(m2+n2)・cos t, n = √(m2+n2)・sin
m n
即ち cos t = ───── ,sin t = ───── …… (3
√(m2+n2) √(m2+n2)
|
|
program Show_Functions(input,output);
(* 坂本 正彦 : 導関数の描画 *)
uses Crt, graph, Turtle1;
var 省略
function fx1( x : real ) : real;
begin
fx1 := m*sin(x) + n*cos(x);
end;
function fx2( x : real ) : real;
begin
fx2 := k*sin(x+t);
end ;
procedure Shokichi; 省略
procedure Ten; 省略
procedure Draw_Function1;
var i, x, y : real;
begin
i := -x_range;
y := 0; end.
|
while i <= x_range do
begin
x := i; y := fx1(x);
if abs(y)<= y_range then
Ten( round(200*x/x_range),
round(200*y/y_range),col);
i := i + sg_d;
end;
end;
procedure Draw_Function2; 省略
procedure Zahyojiku; 省略
begin (* MainProgram *)
Initturtle;
Shokichi; Zahyojiku;
m := 3; n := 4;
col := blue; Draw_Function1;
k := 5; t := 0.93;
col := red; Draw_Function2;
end.
|
 平成8年度市販ソフト実践事例集II
平成8年度市販ソフト実践事例集II