 |
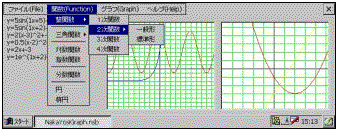
| �}2�@�O���t�\���\�t�g |
(1) ���w�T�C�u2�����v�̎w��
�@�O���܂ł�1�����K��2�����̈�ʌ`�ƕW���`�ɂ��Ċw�B�{����2����y=a(x�|��)(x�|��)�̃O���t�̐����ɂ��Ċw�ԁB���k�Ɂuy=2(x�|1)(x�|3)�͂ǂ̂悤�ȃO���t�ɂȂ邩�v�Ɩ₤�ƁC�u�������ɂȂ�v�Ɠ����鐶�k�͏��Ȃ��C�^����ꂽ���̎��ɂ�2���Ȃ��̂ŁC�ނ��뒼���I�Ɂu�����ɂȂ�v��u�܂���ɂȂ�v�Ɠ����鐶�k�̂ق������������B�����ŁC�܂��͂��̃O���t�����ۂɒ��ׂĂ݂邱�Ƃɂ����B
�@����J���������g�ђ[���p�̃O���t�\���\�t�g(�}2)��2�����ɂ��Ă͈�ʌ`�ƕW���`�����\���ł��Ȃ��B���̂��߁C�ǂ��炩�̌`�ɕό`���Ȃ���Ȃ�Ȃ��B���k�͂܂��Ή��\���쐬���O���t���菑�������B���̌�C��ʌ`�ɕό`�����g�ђ[�����g���ăO���t��\�������菑���̃O���t���m���߂��B�O���t����肭�����Ȃ��������k�͕\���������O���t�����ƂɏC�����C�ǂ̂悤�Ȑ��������邩�ׂ��B���̌�C����ꂽ���������̊��̎��̏ꍇ�ł����Ă͂܂邩�ǂ��������̃O���t�\���\�t�g�Ŋm���߂��B
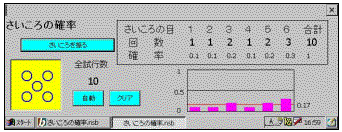 |
| �}3�@�T�C�R���̊m�� |
�@���g�ђ[�������p���邱�ƂŁC�O���t�̍쐬�Ɏ��Ԃ��Ƃ�ꂸ�C���̃O���t�̐����̍l�@�Ɏw�����œ_�����邱�Ƃ��ł���(�w�����e�̏œ_��)�B�܂��C���m�ɃO���t���`���邱�Ƃł��̐��������o�I�ɗ������邱�Ƃ��ł���(���̎��o��)�B�w�K�����̗L���ȓ���Ƃ��Ċ��p�ł������̂Ǝv����B
(2) ���w�T�C�u�m���v�̎w�� �@
�@�܂����߂ɁC�����̃T�C�R�����g���āC��������1����6�̖ڂ̑��Γx�����v�Z�����B���s�����Ȃ��Ƒ��Γx���ɕ肪�ł��B�����ŁC�J�������u�T�C�R���̊m���v�Ƃ�������(�}3)���g���āC���s�ɂ����1����6�̖ڂ̑��Γx�����ǂ̂悤�ɕω����邩�������E�ώ@�����B���̋��ނ̉�ʂ͏��g�ђ[�����t���v���W�F�N�^�ɐڑ����邱�ƂŃN���X�S�̂ł̋��L���\�ł���(�}4)�B
 |
| �}4�@���H�̗l�q |
�@���g�ђ[���ł̎����͎��ۂ̎����ł͕s�\�ȑ�����̎��s���u���ɍs�����Ƃ��ł��������ʂ̍l�@�ɏ\���Ȏ��Ԃ��m�ۂ��邱�Ƃ��ł���(�w�����e�̏œ_��)�B�܂��C�����̌��ʂ������ɐ��l�ƃO���t�Ō��邱�Ƃ��ł��C���s�Ƒ��Γx���̕ω��̗l�q�����o�I�ɗ������邱�Ƃ��ł������̂Ǝv����(���̎��o��)�B�܂��C�l�@���ʂk�����\����Ƃ��̓v���W�F�N�^�ɐڑ����邾���Ńv���[���e�[�V�����̓���Ƃ��Ă����p���ł���(�}4)�B
(3)���B�C�u�R���s���[�^�ɂ�������̏����v�̎w��
�@�w�����e�͐V���ȁu���B�v��z�肵�����̂ł��邪�C���ۂ̎��H�͐�U�Ȃ̊w�Z�ݒ�Ȗځu���Z�p���p�v�ōs�������̂ł���B�O��܂ł͎l�����Z�╪��̃A���S���Y���ɂ��ĊȒP�Ȏ����ʂ��Ċw��ł���B���������Ƃɍ���͂�����g�ݍ��킹���A���S���Y�����l���v���O������g�ފw�K�����ł���(�}5)�B�t���[�`���[�g�ɂ͊ȒP�ɏ����\�����Ƃ��ł������C�v���O�����ɂ͎��Ԃ�K�v�Ƃ����B���ɃC�x���g�h���u���^�ł��邽�߁C������x�̊��ꂪ�K�v�ł���Ǝv��ꂽ�B�������C���g�ђ[���Ńv���O��������f�o�b�O�܂ōs���邽�߁C����Ƀp�\�R����\�t�g�E�F�A���Ȃ����k���C����Ɏ����A���Ă����ɑ������ł���ȂǁC�w�K�̌p������ۂ��Ƃ��ł����B�܂��C���g�ђ[���̓p�\�R���̕⏕�Ƃ������͂ނ���p�\�R���Ɠ��l�Ɏg�p�ł�����̂Ǝv����B
|



